Дополнительные задания
Пример 9. Задача об остроугольном треугольнике. На окружности случайно выбираются три точки. Какова вероятность того, что треугольник с вершинами в этих точках - остроугольный? (См. рис. 41).
Решение
Ясно, что при любом повороте окружности вероятности событий и условие "остроугольности" сохраняются; так что мы можем считать, что одна из трех выбираемых вершин A, B, C - скажем, C - фиксирована, а две другие уже выбираются случайно. Будем задавать их положения величинами дуг CA = a, CB = b, отсчитываемых против часовой стрелки. Будем измерять дуги в радианах, тогда пара (a, b) - это точка в квадрате 0 < a < 2Pi, 0 < b < 2Pi. По теореме о том, что величина вписанного угла измеряется половиной дуги между его сторонами, углы треугольника ABC равны Pi-b/2, a/2 и (b-a)/2 (мы считаем, что b>a; случай a>b совершенно аналогичен - a и b меняются ролями). Точки (a, b) в треугольнике a<b<Pi, для которых все три угла A, B, C меньше Pi/2, т.е. b>Pi, a<Pi и b-a<Pi, заполняют внутренность меньшего треугольника, образуемого средними линиями большего. Ситуация в нижнем треугольнике b<a<Pi симметрична относительно диагонали a=b квадрата. Поэтому искомая вероятность равна
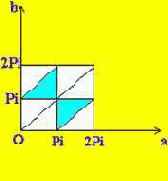
Рис. 41
Program Problem9;
uses WinCrt;
var
x, y, p, e, pp : real;
i, n, m : longint;
{-------------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{-------------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{-------------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random*2*pi; y := random*2*pi;
if ((y > pi) and (y < x + pi) and (x < pi)) or
((y < pi) and (y > x - pi) and (x > pi))
then m := m + 1
end;
p := m/n;
writeln('Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
155. На отрезке [0; 1] случайно выбираются три числа. Какова вероятность того, что а) выбранное последним число наибольшее? б) числа идут в порядке возрастания?
Пример 10. Какова вероятность того, что при двух бросаниях кубика выпадут а) два числа с суммой не меньше 10? б) два числа, из которых первое делится на второе?
Идея решения задачи проста. Каждое из двух бросаний мы смоделируем, как получение двух случайных чисел из промежутка [1; 6]. (Число очков на игральном кубике следующее: 1, 2, 3, 4, 5, 6).
Для получения таких чисел можно использовать функции:
x := random(6) + 1 и y := random(6) + 1.
"Бросать" кубик будем не два раза, а количество бросаний предоставим устанавливать пользователю. Из "выпавших" чисел x и y будем подсчитывать число случаев, когда: а) x + y > +10; б) x mod y = 0.
Это число случаев разделим на общее число бросаний и получим искомую вероятность (фактически мы получим частоту появления событий о чём речь шла выше).
Программы
Program Problem10a;
uses WinCrt;
var
x, y, p, e, pp : real;
i, n, m : longint;
{-------------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{-------------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{-------------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random(6) + 1; y := random(6) + 1;
if (x + y >= 10) then m := m + 1
end;
p := m/n;
writeln('Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
Program Problem10b;
uses WinCrt;
var
p, e, pp : real;
x, y, i, n, m : longint;
{----------------------------------------------------------------------------------------}
{ Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random(6) + 1; y := random(6) + 1;
if x mod y = 0 then
m := m + 1
end;
p := m/n;
writeln('Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
156. Какова вероятность, что при первом бросании выпадет не меньше 5 очков, а при втором - не меньше 4?
157. Какова вероятность, что хотя бы при одном из двух бросаний кубика выпадет не менее 5 очков?
158. Какова вероятность, что количество очков, выпавших при двух бросаниях, отличаются не более чем на 1?
159. (Случайные числа и точки: равномерное распределение). Найдите вероятность того, что сумма x + y, где x, y - случайные числа на отрезке [0; 1], больше данного числа a.
160. На отрезке [0; 1] случайно выбираются три числа. Какова вероятность того, что а) выбранное последним число наибольшее? б) числа идут в порядке возрастания?
161. На окружности случайно выбраны четыре точки A, B, C, D. Какова вероятность того, что отрезки AC и BD пересекаются?
162. а) В окружности проведен диаметр. На нём случайно выбирается точка и через нее проводится хорда, перпендикулярная диаметру. Какова вероятность, что длина хорды больше радиуса окружности?
б) На окружности случайно выбираются две точки. Какова вероятность, что длина соединяющей их хорды больше радиуса?
в) В круге случайно выбрана точка. Какова вероятность, что хорды с серединой в этой точке больше радиуса?
г) Решите аналогичные задачи про хорду длины r

Замечание. Задачи а), б), в) как бы три варианта одной и той же: проведем случайную прямую, пересекающую окружность: какова вероятность, что длина высекаемой хорды больше радиуса? Но ответ в них разный (парадокс Бертрана)!
163. На окружности случайно выбраны три точки.
Какова вероятность, что у треугольника с вершинами в этих точках: а) есть угол больше 30 градусов? б) все углы больше 30 градусов? в) все углы меньше 120 градусов?
164. На отрезке случайно выбраны две точки. Какова вероятность, что из отрезков, на которые он разбит, можно составить треугольник?
165. Плоскость разбита сеткой прямых на а) квадраты; б) правильные треугольники со стороной 1. Какова вероятность, что монета диаметра 1, случайно брошенная на плоскость, закроет одну из вершин сетки?
166. Найдите вероятность того, что а) выпуклый n-угольник с вершинами в случайных точках окружности содержит ее центр?
б) Докажите, что вероятность того, что n случайно выбранных точек на сфере лежат на одной полусфере (по одну сторону от некоторого большого круга) равна (n2 - n + 2)/2n.
Ответы
К заданию 2
Так как общее число карточек равно 7, то их можно упорядочить 7! способами. Поскольку обе буквы Т и обе буквы Р можно менять местами, не изменяя слова, то слово ТРАКТОР получится
2!.2! раза. Искомая вероятность равна:

Иначе тот же результат можно было бы получить, заметив, что в результате извлечения карточек мы получаем перестановку с повторениями состава (2, 2, 1, 1, 1), причем все такие перестановки имеют одну и ту же вероятность. Так как число перестановок равно P(2, 2, 1, 1, 1), то вероятность каждой из перестановок
равна

Program problem2;
uses WinCrt;
var
p : real;
k1, k : integer;
{----------------------------------------------------------------------------------------}
Procedure fakt(n : integer; var f : integer);
var
i : integer;
begin
f := 1;
if n = 0 then f := 1
else for i := 1 to n do
f := f*i
end;
{----------------------------------------------------------------------------------------}
begin
fakt(7, k); fakt(2, k1);
p := (k1*k1)/k;
writeln('Вероятность получ. слова "трактор" равна ', p:10:8)
end.
К заданию 3
Приведем лишь математическое решение задачи. Последующее составление программы достаточно простое.
Вычислить: P4(3) и P6(4).
По формуле Бернулли


Далее необходимо сравнить полученные результаты и сделать вывод.
К заданию 4 (пример 1)
{ Биномиальный закон распределения вероятностей }
Program Problem4_1;
uses WinCrt;
var
p, pp : real;
n, i : integer;
{----------------------------------------------------------------------------------------}
{ Процедура возведения в степень }
Procedure
Extent(a : real; n : integer; var e : real);
var
i : integer;
begin
e := 1;
if n = 0 then e := 1
else for i := 1 to n do e := e*a
end;
{----------------------------------------------------------------------------------------}
{ Рекуррентная процедура вычисления биномиального закона }
{ распределения }
Procedure Recurro_binomial(n, k : integer; p : real; var pp : real);
var
i : integer;
begin
Extent(1 - p, n, pp);
for i := 1 to k do pp := (pp*(n - i + 1)*p)/(i*(1 - p))
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите общее число рождений '); readln(n);
write('Введите вероятность рождения мальчика '); readln(p);
writeln('Биномиальный закон распределения вероятностей');
writeln;
for i := 0 to n do
write(i:6, ' '); writeln; writeln;
for i := 0 to n do
begin
Recurro_binomial(n, i, p, pp); write(pp:1:4, ' ')
end;
writeln; writeln;
Recurro_binomial(10, 6, p, pp);
writeln('Вероятность того, что из 10 наугад выбранных');
writeln('рождений будет 6 мальчиков, равна ', pp:1:6)
end.
К заданию 7
{ Распределение Пуассона }
Program Problem7;
uses WinCrt;
var
n, m : longint;
p, a : real;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления вероятности распределения Пуассона }
Function PS(m : integer; a : real) : real;
var
i : integer;
pp : real;
begin
pp := exp(-a);
if m = 0 then pp := exp(-a)
else for i := 1 to m do pp := pp*a/i;
PS := pp
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите общее число изделий '); readln(n);
write('Введите вероятность изделия быть бракованным ');
readln(p);
writeln('Введите число бракованных изделий, вероятность ');
write('появления которых Вы находите '); readln(m);
a := n*p;
writeln('Вероятность ', m, ' бракованных изделий в ');
writeln('партии из ',n, ' изделий равна ', PS(m, a):1:6)
end.
К заданию 9
{ Применение интегральной формулы Муавра-Лапласа }
Program Problem1;
uses WinCrt;
var
n, m1, m2 : longint;
p, PP : real;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if
x >= 5
then
FF := 1
else if x <= -5
then
FF := -1 else
begin
u := x; n := 0; I := 0;
repeat
I := I + u; n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until
abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисл. вероятн. наст. событ. из промеж. [m1; m2] }
Procedure
Interval(n, m1, m2 : longint; p : real; var PP : real);
var
x1, x2 : real;
begin
x1 := (m1 - n*p)/sqrt(n*p*(1 - p));
x2 := (m2 - n*p)/sqrt(n*p*(1 - p));
PP := (FF(x2) - FF(x1))/2
end;
{----------------------------------------------------------------------------------------}
{ Основная программа. Число бракованных изделий из промежутка }
begin
write('Введите общее число изделий '); readln(n);
write('Введите вероятность наступление одного события ');
readln(p);
write('Введите левую границу промежутка '); readln(m1);
write('Введите правую границу промежутка '); readln(m2);
Interval(n, m1, m2, p, PP);
writeln('Вероятность того, что число бракованных изделий');
write('находится в промежутке [',m1, '; ', m2, '] равна ');
writeln(PP:1:8)
end.
{ Применение интегральной формулы Муавра-Лапласа }
Program Problem2;
uses WinCrt;
var
n, m1, m2 : longint;
p, q, PP : real;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if
x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u; n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until
abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисл. вероятн. наст. событ. из промеж. [m1; m2] }
Procedure
Interval(n, m1, m2 : longint; p : real; var PP : real);
var
x1, x2 : real;
begin
x1 := (m1 - n*p)/sqrt(n*p*(1 - p));
x2 := (m2 - n*p)/sqrt(n*p*(1 - p));
PP := (FF(x2) - FF(x1))/2
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите общее число изделий '); readln(n);
write('Введите вероятность брака в одном изделии '); readln(q);
write('Введите левую границу промежутка '); readln(m1);
write('Введите правую границу промежутка '); readln(m2);
p := 1 - q;
Interval(n, m1, m2, p, PP);
writeln('Вероятность того, что число пригодных изделий');
write('находится в промежутке [',m1, '; ', m2, '] равна ');
writeln(PP:1:8)
end.
К заданию 10
{ Процедура нахождения числа испытаний n, чтобы обеспечить }
{ заданную вероятность отклонения частоты от np }
Procedure Number(p, e, PP : real; var n : longint);
var
x : real;
begin
x := 0;
repeat
x := x + 0.01
until
FF(x) >= PP;
n := round(e/(x*sqrt(p*(1 - p))) + 0.5);
n := sqr(n)
end;
{ Применение интегральной формулы Муавра-Лапласа }
Program Task10;
uses WinCrt;
var
n : longint;
e, q, PP : real;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if
x >= 5
then
FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until
abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура нахождения числа испытаний n }
Procedure Number(p, e, PP : real; var n : longint);
var
x : real;
begin
x := 0;
repeat
x := x + 0.01
until FF(x) >= PP;
n := round(e/(x*sqrt(p*(1 - p))) + 0.5);
n := sqr(n)
end;
{----------------------------------------------------------------------------------------}
begin
write(' Введите вероятность отклонения клемм от принято');
write('го стандарта '); readln(q);
write('Введите число стандартных клемм отличающихся ');
write('от np (по модулю) '); readln(e);
write('Укажите вероятность этого отклонения '); readln(PP);
Number(q, e, PP, n);
writeln('Искомое число взятых наудачу клемм равно ', n)
end.
К заданию 11
{ Процедура определение границы отклонения (ReIection) частости}
{ от заданной вероятности наступления одного события }
Procedure ReIection(n : longint; p, PP, eps : real; var e : real);
var
x : real;
begin
x := 0;
repeat
x := x + eps
until
FF(x) >= PP;
e := x*sqrt(p*(1 - p)/n)
end;
{ Применение интегральной формулы Муавра-Лапласа }
Program Task3;
uses WinCrt;
var
n : longint;
e, eps, p, pp : real;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if
x >= 5
then
FF := 1
else if x <= -5
then
FF := -1
else
begin
u := x;
n := 0;
I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until
abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура определение границы отклонения (ReIection) частости}
{ от заданной вероятности наступления одного события }
Procedure ReIection(n : longint; p, PP, eps : real; var e : real);
var
x : real;
begin
x := 0;
repeat
x := x + eps
until
FF(x) >= PP;
e := x*sqrt(p*(1 - p)/n)
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите вероятность события в каждом испытании '); readln(p);
write(' Введите общее число произведенных испытаний '); readln(n);
write('Укажите гарантированную вероятность '); readln(PP);
write('Укажите точность вычисления искомой величины '); readln(eps);
ReIection(n, p, PP, eps, e);
writeln('Искомая граница отклонения частости от вероят-');
write('ности будет находиться в промежутке ');
writeln('[', p-e:1:4, '; ', p+e:1:4, ']')
end.
К заданию 12
{ Применение интегральной формулы Муавра-Лапласа }
Program Problem12;
uses WinCrt;
var
n : longint;
e, p, PP : real;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура нахождения числа испытаний n, чтобы обеспечить }
{ заданную вероятность отклонения частности от заданного числа }
Procedure
Number3(p, e, PP : real; var n : longint);
var
x : real;
begin
x := 0;
repeat
x := x + 0.01
until FF(x) >= PP;
n := round((x*sqrt(p*(1 - p))/e) + 0.5);
n := sqr(n)
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write(' Введите постоянную для каждого испытания ');
write('вероятность '); readln(p);
writeln('Введите число, от которого по абсолютной ');
write('величине должна отличаться частость '); readln(e);
write('Укажите гарантированную вероятность '); readln(PP);
writeln;
Number3(p, e, PP, n);
writeln('Число испытаний должно быть больше или равно ', n)
end.
К
заданию 15
Program Normal1;
uses WinCrt;
var
PP, x, l, c : real;
{-----------------------------------------------------------------------------------------}
{ Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until
abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура нахождения аргумента x }
Procedure Argument(PP : real; var
x : real);
begin
x := 0;
repeat
x := x + 0.0001
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
write(' Введите среднее квадратическое отклонение '); readln(c);
write('Введите вероятность попадания в интервал, симметричн. M(X) ');
readln(PP);
Argument(PP, x);
l := 2*c*x;
writeln('Длина искомого интервала равна ', L:4:6)
end.
Ответ к задаче 2 задания
Указание
По формуле (6) находим

Ответ
0.06.
Program Exercise_Normal2;
uses WinCrt;
var
PP, x, a, d, e, c : real;
{----------------------------------------------------------------------------------------}
{ Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until
abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура нахождения аргумента x }
Procedure Argument(PP : real; var
x : real);
begin
x := 0;
repeat
x := x + 0.0001
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите среднее значение ');
writeln('нормально распределенной случайной величины a = M(X) ');
write('т.е. средний диаметр детали '); readln(a);
write('Введите дисперсию '); readln(d);
writeln('Введите гарантированную вероятность');
write(' отклонения детали от среднего размера '); readln(PP);
Argument(PP, x);
c := sqrt(d);
e := c*x;
writeln('Максимальное отклонение диаметра от среднего равно ', e:2:6)
end.
Ответ к задаче 3 задания
а) 0.9986; б) 0.7823.
Program Exercise_Normal13a;
uses WinCrt;
var
e, c, d, pp, p1, sum : real;
n, m, i : integer;
{----------------------------------------------------------------------------------------}
{ Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура возведения в степень }
Procedure Extent(a : real; n : integer; var e : real);
var
i : integer;
begin
e := 1;
if n = 0 then e := 1 else for i := 1 to n do
e := e*a
end;
{--------------------------------------------------------------------------------------}
{ Рекуррентная процедура вычисления вероятности }
{ биномиального закона распределения }
Procedure Recurro_binomial(n, m : integer; p : real; var p1 : real);
var
i : integer;
begin
Extent(1 - p, n, p1);
for
i := 1 to m do p1 := (p1*(n - i + 1)*p)/(i*(1 - p))
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите дисперсию '); readln(d); c := sqrt(d);
write(' Введите отклонение детали от заданного размера '); readln(e);
write('Введите число измерений '); readln(n);
write('Введите допускаемое число появления ощибок '); readln(m);
pp := 1 - FF(e/c);
sum := 0;
for i := 0 to m do
begin
Recurro_binomial(n, i, pp, p1);
sum := sum + p1
end;
writeln('Вероятность брака равна ', sum:1:6)
end.
К
заданию 16
Program Task16_1;
uses WinCrt;
var
x, y, p, e, pp : real;
i, n, m, a, b : longint;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u; n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1; x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите длину отрезка - a = '); readln(a);
write('Введите расстояние b от точки A '); readln(b);
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random*a; y := random*a;
if (x <= b) and (y <= b) then m := m + 1
end;
p := m/n;
writeln('Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
Program Task16_2;
uses WinCrt;
var
x, y, p, a, q, k1, h, e, pp : real;
i, n, k, m : longint;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u; n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1; x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите длину стороны BC '); readln(a);
write('Введите высоту трапеции '); readln(h);
write('Введите величину угла BAE < Pi/2 в рад '); readln(q);
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
k := 0; m := 0; k1 := sin(q)/cos(q);
for i := 1 to n do
begin
x := random*(2*h/k1 + a); y := random*h;
if (y < k1*x) and (y < -k1*x + k1*(2*h/k1 + a)) then k := k + 1;
if ((x < h/k1) and (y < k1*x)) or
((x > a + h/k1) and
(y < -k1*x + k1*(2*h/k1 + a))) then m := m + 1
end;
p := m/k;
writeln('Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
К заданию 17
Пусть событие E - точка оказалась внутри куба с ребром, равным 3 см. Будем считать, что исходы испытания распределены равномерно. Тогда вероятность наступления события E пропорциональна мере этого куба и равна:

V2 - объем параллелепипеда.
Program Task17;
uses WinCrt;
var
x, y, z, p, e, pp : real;
i, n, s : longint;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
s := 0;
for i := 1 to n do
begin
x := random*4; y := random*6; z := random*10;
if (x < 3) and (y < 3) and (z < 3) then s := s + 1
end;
p := s/n;
writeln('Вероятность появление точки внутри куба ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
К
заданию 18
Program Task18_1;
uses WinCrt;
var
x, y, p, e, pp : real;
i, n, m : longint;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random*12;
y := random*12;
if (y > x - 3) and (y < x + 3) then m := m + 1
end;
p := m/n;
writeln('Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
Program Task18_2;
uses WinCrt;
var
x, y, p, e, pp : real;
i, n, m : longint;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random*20;
y := random*20;
if (y > x - 5) and (y < x + 5) and
(y > x - 2) and (y < x + 2)
then m := m + 1
end;
p := (2*m)/n;
writeln('Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
К
заданию 19
Program Task19;
uses WinCrt;
var
p, x, y, z, e, pp : real;
i, n, m : longint;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random; y := random; z := random;
if ((x < 1/3) and (y > 1/3) and (y < 2/3) and (z > 2/3)) or
((y < 1/3) and (x > 1/3) and (x < 2/3) and (z > 2/3)) or
((y < 1/3) and (z > 1/3) and (z < 2/3) and (x > 2/3)) or
((z < 1/3) and (x > 1/3) and (x < 2/3) and (y > 2/3)) or
((z < 1/3) and (y > 1/3) and (y < 2/3) and (x > 2/3)) or
((x < 1/3) and (z > 1/3) and (z < 2/3) and (y > 2/3))
then m := m + 1
end;
p := m/n;
writeln(' Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
