Классические методы нахождения изолированного корня
На этом занятии мы рассмотрим задачу нахождения корней уравнения
f(x) = 0. (1)
"Изолированным" мы будем называть корень c уравнения (1), если найден, содержащий его промежуток [a, b]: a < c < b, на котором других корней нет.
Для решения задачи уточнения корня, потребуем, чтобы функция удовлетворяла следующим условиям:
1) f(x), f'(x) и f''(x) непрерывны на промежутке [a, b]; 2) значения функции на концах промежутка [a, b] имеют разные знаки:

3) обе производные f'(x) и f''(x) сохраняют каждая определенные знаки на всем промежутке [a, b], это значит, что функция строго монотонна (возрастает или убывает) на этом промежутке. Требование сохранение знака второй производной f''(x) геометрически означает, что график функции вогнутостью обращен всегда в одну сторону и не имеет перегибов.
Столь жесткие требования к поведению функции на промежутке казалось бы сильно сужают круг рассматриваемых функций, но это не так.
Для алгебраических функций всегда можно найти промежуток (если вообще вещественные корни алгебраического уравнения существуют), на котором все три перечисленных условия выполняются.
Что касается трансцендентных уравнений, то на практике в большинстве случаев перечисленные условия выполняются и для них.
Во всяком случае, круг уравнений достаточно широк, чтобы заняться рассмотрением ниже приводимых приемов решения, тем более что эти способы являются классическими и полезны будут даже из соображений общего развития читателей.
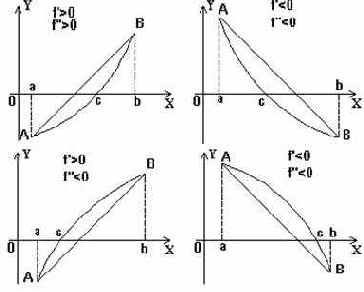
Рис. 44
На рисунке 44 изображены четыре возможные случая, отвечающие различным комбинациям знаков f'(x) и f''(x).
1-й случай, когда f'(x)>0 - функция возрастает на промежутке, f''(x) > 0 - график вогнутостью направлен вверх.
2-й случай: f'(x)<0 - функция убывает, f''(x)>0 - вогнутость вверх.
3-й случай: f'(x) > 0 - функция возрастает, f''(x) < 0 - вогнутость направлена вниз.
4-й случай: f'(x) < 0 - функция убывает, f''(x) < 0 - вогнутость вниз.
1.1. Метод хорд (правило пропорциональных частей)
Пусть c - корень уравнения f(x) = 0 на промежутке [a, b], тогда c - абсцисса точки пересечения кривой с осью ox. Конечная задача - найти эту точку или как можно близкое значение абсциссы к этой точки.
Рассмотрим случаи 1-й и 3-й, когда хорда находится слева от кривой и пересекает ось x между точками a и c (см. рис. 45).
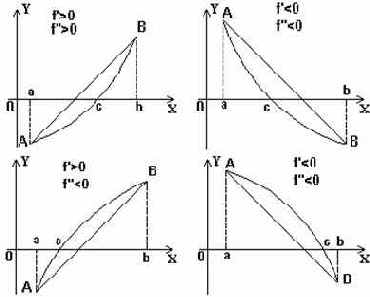
Рис. 45
Заменим кривую AcB хордой AB. Мы сможем написать уравнение этой хорды, а значит найти ее точку пересечения с осью x.
Уравнение хорды - это уравнение прямой, проходящей через две точки (a, f(a)) и (b, f(b)).
Общий вид уравнения прямой, проходящей через две точки такой:

Подставляя в эту формулу значения, получим уравнение хорды AB:


Пусть x1
- точка пересечения хорды с осью x, так как y = 0, то

x1 может считаться приближенным значением корня. Для более точного его определения рассмотрим промежуток [x1, b]. И на этом промежутке заменим кривую хордой A1B и найдем новое приближение к корню - x2:

Для n + 1 - го приближения получим:

Этот процесс можно продолжать сколь угодно долго и построить возрастающую последовательность приближенных значений корня:
a < x1
< x2 < ... < xn < xn+1 < ... < c.
В математическом анализе доказывается, что переменная xn с ростом n стремится к c, т.е. c является пределом этой последовательности.
Для случаев 2-го и 3-го, когда хорда располагается справа от кривой (см. рис. 46), и пересекает ось ox между точками с и b, значения приближенных значений корней будут следующими:
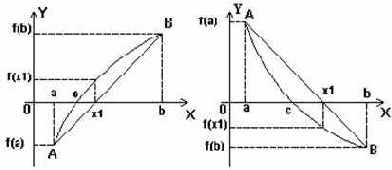
Рис. 46


....................................,

В результате получим убывающую последовательность, которая также сходится к c:
b > x1
> x2 > ... > xn > xn+1 > ... > c
Во всех случаях можно найти корень с любой степенью точности.
Как оценивается точность приближенного значения xn?
По формуле Лагранжа (формуле конечных приращений) для разности




Так как f(c) = 0, то получим:

Если обозначить через m наименьшее значение |f'(x)| на промежутке [a, b], которое можно определить заранее, то получим формулу для оценки точности вычисления корня:


где eps - заданная точность вычисления. Пользуясь рекуррентной формулой (1) и формулой для оценки точности вычисления, нетрудно составить процедуру уточнения корня методом хорд:
{ Процедура уточнения корня методом хорд }
Procedure chord(a, b, eps, min : real; var
x : real);
var
x1 : real;
begin
x1 := a;
repeat
x := x1 - ((b - x1)*fx(x1))/(fx(b) - fx(x1));
x1 := x
until abs(fx(x))/min < eps
end;
Для оценки точности вычисления корня необходимо вычислять наименьшее значение производной f'(x) на промежутке [a, b], поэтому возникает необходимость в нахождении значения производной в точке и здесь мы приходим к задаче численного дифференцирования.
1.2. Вычисление производных (численное дифференцирование)
При вычислении производной функции, будем иметь в виду, что один из способов найти производную



Таким образом, вычисляется производная в середине промежутка.
По значениям f' можно таким же способом найти производную от f', т.е. f''. Можно выразить f'' непосредственно через f(x):


Для производной третьего порядка можно использовать следующую формулу:

Возникают естественные вопросы, откуда происходят эти формулы и как оценивать точность вычисления производных по этим формулам?
Формулы являются результатом дифференцирования интерполяционных многочленов Ньютона и других. Сущность которых состоит в том, что заданная функция f(x) представляется в виде многочлена, который значительно проще дифференцировать, чем какие-либо другие функции, особенно трансцендентные или представляющие собой сложные выражения. Как получаются такие многочлены, мы узнаем позже - этому вопросу будет посвящена полностью глава, а сейчас ограничимся лишь результатами, которые нам необходимы в этой главе.
Оценка погрешности и точности вычисления не менее серьезный и сложный процесс, чем само приближенное вычисление.
Так для оценки погрешности дифференцирования могут быть применены следующие формулы:

где предполагается, что функция f(x) дифференцируемая n + 1 раз, а точка

На практике f
(n+1)(c) оценивать непросто, поэтому при малых dx приближенно полагают:

и тогда получается следующая формула

Мы будем пользоваться формулой (2), а впоследствии и формулой (3), в зависимости от конкретной задачи и тех сложностей, которые могут возникнуть при составлении программ.
Используя эти формулы, составим функцию для вычисления первой производной. Точность вычисления eps задается пользователем, а первоначальная величина промежутка dx устанавливается 1, а затем, для уточнения вычисления - делится на 2. Впрочем, читатель может предложить другие способы изменения промежутка dx, когда значительно быстрее достигается вычисление производной с заданной степенью точности.
{ Вычисление 1-й производной и опред. точности ее вычислен.}
{ derivative - производная }
Function derivat1(x0, eps : real) : real;
var
dx, dy, dy2 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx/2) - fx(x0 - dx/2);
dy2 := fx(5*x0/4 + dx) - 2*fx(5*x0/4);
dy2 := dy2 + fx(5*x0/4 - dx)
until abs(dy2/(2*dx)) < eps;
derivat1 := dy/dx
end;
Здесь, для определения точности вычисления, используется вторая производная в точке

Запись ее вычисления выполнена в две строки только из-за лучшей наглядности написания программы.
Возможен и другой вариант написания функции с использованием формулы (3) для оценки точности вычисления.
Тогда функция запишется так:
{ Вычисление 1-й производной и опред. точности ее вычислен.}
{ derivative - производная }
Function derivat1(x0, eps : real) : real;
var
dx, dy, dy2 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx/2) - fx(x0 - dx/2);
dy2 := fx(5*x0/4 + dx) - 2*fx(5*x0/4);
dy2 := dy2 + fx(5*x0/4 - dx)
until abs((dy2*dy2*fx(x0))/(2*dx)) < eps;
derivat1 := dy/dx
end;
Задание 1
Составьте самостоятельно функции для вычисления второй производной и проверьте ее работу в программах для вычисления второй производной функций:

Однако вернемся к задаче решения уравнения методом хорд. Имея возможность вычислить значение производной, можно составить процедуру определения модуля ее наименьшего значения на промежутке [a, b].
Для этого достаточно сравнить модуль значения производной на концах промежутка и выбрать среди этих двух значений меньшее (такое право дает нам сделать тот факт, что по условию, функция на промежутке строго монотонна вместе со своими производными первого и второго порядков). Процедура получится простой:
{ Процедура определения наименьшего значения производной }
Procedure
minimum(a, b, eps : real; var min : real);
begin
min := abs(derivat1(a, eps));
if min > abs(derivat1(b, eps))
then min := abs(derivat1(b, eps))
end;
Но и построенная таким образом процедура имеет очень существенный недостаток! А если в точке a или b производная будет равна нулю? Тогда деление на нуль станет невозможным и в программе будет получена ошибка. Чтобы избежать этого, изменим процедуру так, чтобы в случае равенства нулю производной в одной и точек a или b находилось бы ее значение в ближайшей окрестности этой точки. Но, для точки a брать значение слева нельзя, оно выйдет за пределы промежутка [a, b], также, как и справа от точки b. Поэтому следует брать значение очень близкое к a, но справа от нее, аналогично для точки b - брать близкое значение слева от b.
Процедуру
можно построить так:
{ Процедура определения наименьшего значения производной }
{ на заданном промежутке }
Procedure minimum(a, b, eps : real; var min : real);
var
d : real;
begin
a := a - eps;
b := b + eps;
repeat
a := a + eps;
b := b - eps;
min := abs(derivat1(a, eps));
d := abs(derivat1(b, eps));
if min > d then min := d
until min <> 0
end;
Объединяя полученные функции и процедуры в одну программу, мы получим программу вычисления корня уравнения на изолированном промежутке методом хорд.
{ Решение уравнений методом хорд. method - метод, chord - хорда }
Program Method_Chord;
uses WinCrt;
var
a, b, x, min, eps : real;
{--------------------------------------------------------------------------------------}
{ Заданная функция }
Function fx(x : real) : real;
begin
fx := x*x*x - 2*x*x - 4*x - 7
end;
{--------------------------------------------------------------------------------------}
{ Вычисление 1-й производной }
{ derivative - производная }
Function derivat1(x0, eps : real) : real;
var
dx, dy, dy2 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx/2) - fx(x0 - dx/2);
dy2 := fx(5*x0/4 + dx) - 2*fx(5*x0/4);
dy2 := dy2 + fx(5*x0/4 - dx)
until abs(dy2/(2*dx)) < eps;
derivat1 := dy/dx
end;
{----------------------------------------------------------------------------------------}
{ Процедура определения наименьшего значения производной }
{ на заданном промежутке }
Procedure minimum(a, b, eps : real; var min : real);
var
d : real;
begin
a := a - eps;
b := b + eps;
repeat
a := a + eps;
b := b - eps;
min := abs(derivat1(a, eps));
d := abs(derivat1(b, eps));
if min > d then min := d
until min <> 0
end;
{----------------------------------------------------------------------------------------}
{ Процедура уточнения корня методом хорд }
Procedure chord(a, b, eps, min : real; var
x : real);
var
x1 : real;
begin
x1 := a;
repeat
x := x1 - ((b - x1)*fx(x1))/(fx(b) - fx(x1));
x1 := x
until abs(fx(x))/min < eps
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите левый конец промежутка a = '); readln(a);
write('Введите правый конец промежутка b = '); readln(b);
write('Введите точность вычисления корня eps = ');
readln(eps);
minimum(a, b, eps, min);
chord(a, b, eps, min, x);
writeln('Корень уравнения равен x = ', x:12:12);
writeln('С точностью до eps = ', eps:1:12)
end.
И в этих программах будем применять уже известную нам функцию для указания точности вычисления.
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
Добавим эту функцию в программу.
{ Решение уравнений методом хорд. method - метод, chord - хорда}
{ Правило пропорциональных частей }
Program
Method_Chord;
uses WinCrt;
var
a, b, x, min, eps : real;
{----------------------------------------------------------------------------------------}
{ Заданная функция }
Function fx(x : real) : real;
begin
fx := x*x*x - 2*x*x - 4*x - 7
end;
{----------------------------------------------------------------------------------------}
{ Вычисление 1-й производной }
{ derivative - производная }
Function derivat1(x0, eps : real) : real;
var
dx, dy, dy2 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx/2) - fx(x0 - dx/2);
dy2 := fx(5*x0/4 + dx) - 2*fx(5*x0/4);
dy2 := dy2 + fx(5*x0/4 - dx)
until abs(dy2/(2*dx)) < eps;
derivat1 := dy/dx
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Процедура определения наименьшего значения производной }
{ на заданном промежутке }
Procedure minimum(a, b, eps : real; var min : real);
var
d : real;
begin
a := a - eps;
b := b + eps;
repeat
a := a + eps;
b := b - eps;
min := abs(derivat1(a, eps));
d := abs(derivat1(b, eps));
if min > d then min := d
until min <> 0
end;
{----------------------------------------------------------------------------------------}
{ Процедура уточнения корня методом хорд }
Procedure chord(a, b, eps, min : real; var
x : real);
var
x1 : real;
begin
x1 := a;
repeat
x := x1 - ((b - x1)*fx(x1))/(fx(b) - fx(x1));
x1 := x
until abs(fx(x))/min < eps
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите левый конец промежутка a = '); readln(a);
write('Введите правый конец промежутка b = '); readln(b);
write(' Введите точность вычисления корня eps = ');
readln(eps);
minimum(a, b, eps, min);
chord(a, b, eps, min, x);
writeln('Корень уравнения равен x = ', x:6:t(eps));
writeln('С точностью до eps = ', eps:1:t(eps))
end.
1.3. Правило Ньютона (метод касательных)
Будем по прежнему считать, что функция f(x) удовлетворяет всем перечисленным ранее требованиям и искомый корень c изолирован на промежутке [a, b], т. е. a < c < b.
Если в предыдущем примере была предпринята замена кривой, - графика функции, хордой, то возникает естественная идея, а почему бы не заменить ее касательной, проведенной первоначально из точек A или B.
Этот метод носит название правило Ньютона или метод касательных.
Также возможны четыре случая, которые представлены на рисунке 47.
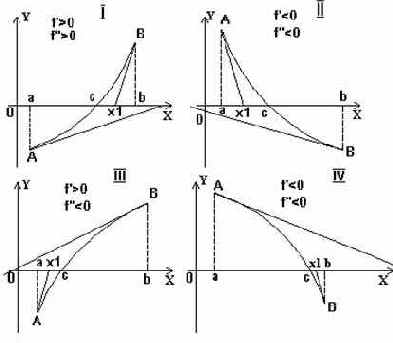
Рис. 47
Рассмотрим уравнение касательной, проведенной в точке B с абсциссой b. Уравнение касательной в этой точке составить нетрудно, оно будет таким:

зная, что в точке пересечения с осью ox y = 0, найдем из уравнения значение x, получим:

Таким образом, мы получаем приближенное значение корня

Возникает вопрос, где лежит точка x1, полученная по формуле (3). Ведь из рисунка следует, что в случаях 2 и 3 она может лежать вообще за пределами промежутка.
В математическом анализе доказывается, что если значение f(b) одного знака с f''(x) - это случаи 1 и 4, то x1 лежит между корнем c и точкой b.
Аналогично, если исходить из точки a, и касательную к кривой провести в точке A, то получим следующую формулу для приближенного значения корня

Также и здесь доказывается, что если f(a) и f''(a) одного знака, то x1 лежит между a и c, a < x1 < c (на рисунке это соответствует случаям 2 и 3).
Как и для случая метода хорд можно построить для 1-го и 4-го случаев убывающую последовательность значений xn сходящейся к c:
b > x1
> x2 > ... > xn > xn+1 > ... > c,
а для случаев 2 и 3 возрастающую последовательность значений также сходящихся к c: a < x1 < x2
< ... < xn < xn+1 < ... < c.
Вычисление значений членов последовательности производится по следующей рекуррентной формуле:

Надо иметь ввиду, что для выбора первоначального значения x (x = a или x = b), надо установить, где знак функции f(x) совпадает со знаком f''(x).
Оценка точности приближения происходит также, как и для случая метода хорд по значению отношения

Исходя из высказанных соображений составим процедуру уточнения корня методом касательных.
{ Процедура уточнения корня методом касательных }
Procedure tangent(a, b, eps, min, dy : real; var x : real);
var
x1 : real;
begin
x1 := a;
repeat
x := x1 - fx(x1)/derivat1(x1);
x1 := x
until abs(fx(x))/min < eps
end;
Для установления первоначального значения x (конца промежутка, от которого начнется уточнения корня) нам нужна будет вторая производная. Функцию, которая ее вычисляет вы должны были составить самостоятельно, а сейчас проверьте себя:
{ Функция вычисления второй производной }
Function
derivat2(x0, eps : real) : real;
var
dx, dy, dy3 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx) - 2*fx(x0) + fx(x0 - dx);
dy3 := fx(5*x0/4 + 2*dx) - 2*fx(5*x0/4 + dx);
dy3 := dy3 - fx(5*x0/4 - 2*dx) + 2*fx(5*x0/4 - dx)
until abs(dy3/(6*dx)) < eps;
derivat2 := dy/(dx*dx)
end;
Программа
{ Решение уравнений методом касательных. method - метод }
{ tangent - касательная. Правило пропорциональных частей }
Program Method_Tangent;
uses WinCrt;
var
a, b, x, min, eps : real;
{----------------------------------------------------------------------------------------}
{ Заданная функция }
Function fx(x : real) : real;
begin
fx := x*x*x - 2*x*x - 4*x - 7
end;
{----------------------------------------------------------------------------------------}
{ Вычисление 1-й производной }
{ derivative - производная }
Function derivat1(x0, eps : real) : real;
var
dx, dy, dy2 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx/2) - fx(x0 - dx/2);
dy2 := fx(5*x0/4 + dx) - 2*fx(5*x0/4);
dy2 := dy2 + fx(5*x0/4 - dx)
until abs((dy2*dy2*fx(x0))/(2*dx)) < eps;
derivat1 := dy/dx
end;
{----------------------------------------------------------------------------------------}
Function derivat2(x0, eps : real) : real;
var
dx, dy, dy3 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx) - 2*fx(x0) + fx(x0 - dx);
dy3 := fx(5*x0/4 + 2*dx) - 2*fx(5*x0/4 + dx);
dy3 := dy3 - fx(5*x0/4 - 2*dx) + 2*fx(5*x0/4 - dx)
until abs(dy3/(6*dx)) < eps;
derivat2 := dy/(dx*dx)
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Процедура определения наименьшего значения производной }
{ на заданном промежутке }
Procedure minimum(a, b, eps : real; var min : real);
var
d : real;
begin
a := a - eps;
b := b + eps;
repeat
a := a + eps;
b := b - eps;
min := abs(derivat1(a, eps));
d := abs(derivat1(b, eps));
if min > d then min := d
until min <> 0
end;
{----------------------------------------------------------------------------------------}
{ Процедура уточнения корня методом касательных }
Procedure tangent(a, b, eps, min : real; var x : real);
var
x1 : real;
begin
x1 := a;
repeat
x := x1 - fx(x1)/derivat1(x1, eps);
x1 := x
until abs(fx(x))/min < eps
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите левый конец промежутка a = '); readln(a);
write('Введите правый конец промежутка b = ');
readln(b);
write('Введите точность вычисления корня eps = ');
readln(eps);
minimum(a, b, eps, min);
if fx(a)*derivat2(a, eps) > 0
then tangent(a, b, eps, min, x)
else tangent(b, a, eps, min, x);
writeln('Корень уравнения равен x = ', x:6:t(eps));
writeln('С точностью до eps = ', eps:1:t(eps))
end.
Вы обратили внимание, что первая производная вычисляется с определением точности вторым способом через приращение аргумента и приращение функции. Почему это сделано?
Когда выяснялся вопрос о точности вычисления производных, то оговаривалось, что при оценки погрешности первой производной по значению второй производной, точка, в которой вычисляется значение второй производной должна быть отлична от x0 и от точек, которые отстоят от x0 на расстоянии кратном dx. При вычислении корня по методу касательных значение первой производной меняется в зависимости от x1, которое может неожиданно попасть в точку, отстоящую от x0 на расстоянии кратном dx, что недопустимо. Поэтому оценка погрешности выполняется вторым способом.
1.4. Комбинированный метод касательных и хорд
Он состоит в одновременном использовании как метода касательных, так и метода хорд.
Если Вы внимательно следили за вычислениями приближенных значений двумя методами, то вероятно заметили, что если методом хорд последовательность значений, начиная от первоначального значения a - левого конца промежутка, возрастает, то для этого же случая по методу касательных последовательность убывает.
Для других двух случаев получается наоборот. Таким образом, получаемые последовательности сближаются и тем самым, применяя одновременно два метода можно получить более быстрое приближение корня.
Если мы имеем дело со случаем 1, тогда, обозначая приближенные значения по методу хорд x1, а по методу касательных - z1, получим:


тогда, a < x1 < c < z1 < b.
При следующем шаге заменяется в этих формулах a и b через x1 и z1:


Общие формулу для построения приближений будут следующими:


О качестве достигнутого приближения, т.е. о точности, можно судить по величине |zn
- xn| - в этом удобство комбинированного метода.
Необходимо изменить процедуры вычисления приближенных корней уравнения по методу хорд и методу касательных следующим образом:
{ Процедура уточнения корня методом хорд }
Procedure chord(a, b : real; var
x : real);
begin
x := a - ((b - a)*fx(a))/(fx(b) - fx(a))
end;
{----------------------------------------------------------------------------------------}
{ Процедура уточнения корня методом касательных }
Procedure tangent(a, b, eps : real; var
z : real);
begin
z := a - fx(a)/derivat1(a, eps)
end;
В основной программе организовать цикл до выполнения условия

{ Решение уравнений комбинированным методом хорд и касательных }
Program Combination_Method;
uses WinCrt;
var
a, b, x, z, eps : real;
{----------------------------------------------------------------------------------------}
{ Заданная функция }
Function fx(x : real) : real;
begin
fx := x*sin(x) - 0.5
end;
{----------------------------------------------------------------------------------------}
{ Вычисление 1-й производной }
{ derivative - производная }
Function derivat1(x0, eps : real) : real;
var
dx, dy, dy2 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx/2) - fx(x0 - dx/2);
dy2 := fx(5*x0/4 + dx) - 2*fx(5*x0/4);
dy2 := dy2 + fx(5*x0/4 - dx)
until abs((dy2*dy2*fx(x0))/(2*dx)) < eps;
derivat1 := dy/dx
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления второй производной }
Function derivat2(x0, eps : real) : real;
var
dx, dy, dy3 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx) - 2*fx(x0) + fx(x0 - dx);
dy3 := fx(5*x0/4 + 2*dx) - 2*fx(5*x0/4 + dx);
dy3 := dy3 - fx(5*x0/4 - 2*dx) + 2*fx(5*x0/4 - dx)
until abs(dy3/(6*dx)) < eps;
derivat2 := dy/(dx*dx)
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Процедура уточнения корня методом хорд }
Procedure chord(a, b : real; var
x : real);
begin
x := a - ((b - a)*fx(a))/(fx(b) - fx(a))
end;
{----------------------------------------------------------------------------------------}
{ Процедура уточнения корня методом касательных }
Procedure tangent(a, b, eps : real; var
z : real);
begin
z := a - fx(a)/derivat1(a, eps)
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите левый конец промежутка a = '); readln(a);
write('Введите правый конец промежутка b = '); readln(b);
write(' Введите точность вычисления корня eps = ');
readln(eps);
repeat
if fx(a)*derivat2(a, eps) > 0
then
begin
tangent(a, b, eps, z);
chord(b, a, x);
b := z; a := x
end
else
begin
tangent(b, a, eps, z);
chord(a, b, x);
b := x; a := z
end
until abs(z - x) < eps;
writeln('Корень уравнения равен x = ', x:6:t(eps));
writeln('С точностью до eps = ', eps:1:t(eps))
end.
Задание 2
При выполнении задания Вам необходимо использовать программу отделения корней, которая изучалась ранее. Таким образом, задания надо выполнять в таком порядке:
1) графическим путем найти самый "большой" промежуток, на котором может находится один или более корней (это можно сделать "вручную", схематически вычертив графики функции);
2) составить программу, в которой объединяется метод отделения корней (другими словами, нахождение изолированных промежутков) и соответствующий метод уточнения корня (метод хорд, касательных или комбинированный).
1. При решении следующих уравнений используйте для уточнения корня метод хорд:

2. Примените для уточнения корня метод касательных:

Замечание. Последнее уравнение можно преобразовать к виду более удобному для решения: ln(3x ) = ln(3x) или xln3 = ln(3x), xln3 - ln(3x) = 0.
Вообще для вычисления степени ax с любым действительным показателем и любым положительным действительным основанием можно составить отдельную процедуру, основываясь на следующих соображениях:
ax = y, ln(a x) = lny, xlna = lny, y = e xlna, окончательно получаем a = exlnx .
На Паскале это запишется так: exp(x*ln(a)).
3. Для решения следующих уравнений используйте в качестве метода уточнения корней, комбинированный метод:

