Применение ряда Фибоначчи
Пример 2. Определение минимума функции с помощью ряда Фибоначчи.
Ряд Фибоначчи много интересных применений в математике. О некоторых из них мы поговорим позже, а на этом занятии разберем использование этого ряда для поиска минимума функции на заданном промежутке (смотри также В.Ф. Очков, Ю.В. Пухначев, "128 советов начинающему программисту", Москва, 1991 г.).
Для примера рассмотрим функцию

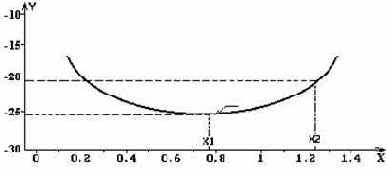
Рис. 23
Итак, стоит задача найти минимум функции на этом промежутке, т.е. значение x, при котором получается минимум и значение функции y в этой точке. Первая мысль, которая возникает - это делить отрезок (0, 2) пополам, затем выяснять, на каком из получившихся частей может находится минимум и делить эту часть пополам и так далее. Такой процесс возможен, но имеет два существенных недостатка.
Во-первых, "приближение" к точке минимума будет очень медленным, придется испробовать много вариантов, чтобы "подобраться" к искомой точке.
Во-вторых, при даже очень большом количестве делений точность приближения будет невелика.
Поэтому, возникает необходимость как-то иначе делить отрезок (если мы избрали метод деления отрезка). Но как? Отделять от одного конца 4-ю или 3-ю части и постепенно сужать отрезок к лучшему результату не приведет, пожалуй еще и к худшему.
Улучшить процесс деления отрезка помогает ряд Фибоначчи. Может даже возникнуть впечатление, что он как будто специально создан для этой цели. Хотя ряд возник совершенно из других более естественных соображений, он показывает число появления кроликов во 2-й, 3-й, 4-й и т. д. годы, если первоначально есть только одна самка и один самец. Но многие закономерности природы прекрасно описываются математическими средствами, вот и в нашем примере ряд Фибоначчи дает очень хорошие результаты.
Для деления отрезка можно задать число делений - n, а затем в зависимости от n определить коэффициент деления, как отношение (n - 1)-го и n-го членов ряда.
Если a - левый конец промежутка, b - правый, тогда разделить отрезок можно так: x2 := a + (b - a)*fib(n - 1)/fib(n); y2 := f(x2);
Для n = 10 отношение fib(9)/fib(10) = 34/55 = 0.6181818... . Тогда, правая граница станет равна: x2 := 1.236364... . Для дальнейшего процесса поиска, надо "приблизить" левый конец промежутка на такое же расстояние к правому концу (

В дальнейшем могут возникнуть несколько случаев.
Если x2 > x1 и y2 > y1, тогда в качестве правого конца промежутка принять x2 и зафиксировать его (b := x2), а x2 заменить на x1 (x2 := x1), y2 присвоить значение y1 (y2:=y1) и повторить процесс приближения левого конца к правому:
x1 := a + b - x2.
Если x2 <= x1 и y2 > y1, тогда a := x2; x2 := x1; y2 := y1 и повторить:
x1 := a + b - x2.
Если x2 > x1 и y2 < y1, тогда a := x1 и выполнить: x1 := a + b - x2.
Если x2 <= x1 и y2 <= y1, тогда b := x1 и выполнить: x1 := a + b - x2.
Если ни одно из этих условий не выполняется, тогда выполнятся оператор:
x1 := a + b - x2
и весь процесс повторяется.
Для составления программы потребуется функция, вычисляющая члены ряда Фибоначчи, уже знакомая нам:
{ Функция вычисления членов ряда Фибоначчи }
Function fib(n : integer) : real;
var
f, f1, f2 : real;
i : integer;
begin
f1 := 1; f := 0;
for i := 1 to n do
begin
f2 := f1; f1 := f;
f := f1 + f2
end;
fib := f
end;
Нужно будет вычислять значения заданной функции и для этого составим следующую функцию:
{ Заданная исследуемая функция }
Function
func(x : real) : real;
begin
func := x*x*x*x - 14*x*x*x + 60*x*x - 70*x
end;
Полностью программа
приводится ниже:
Program Minimumfib;
uses WinCrt;
label 1;
var
a, aa, bb, x, b, x1, x2, y1, y2 : real; i, n : integer;
{----------------------------------------------------------------------------------------}
{ Заданная исследуемая функция }
Function func(x : real) : real;
begin
func := x*x*x*x - 14*x*x*x + 60*x*x - 70*x
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления членов ряда Фибоначчи }
Function fib(n : integer) : real;
var
f, f1, f2 : real; i: integer;
begin
f1 := 1; f := 0;
for i := 1 to n do
begin
f2 := f1;
f1 := f;
f := f1 + f2
end;
fib := f
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите нижнюю границу промежутка '); readln(a);
aa := a;
write('Введите правую границу промежутка '); readln(b);
bb := b;
write('Введите число приближений к минимуму '); readln(n);
x2 := a + (b - a)*fib(n-1)/fib(n); y2 := func(x2);
for i := 1 to n do
begin
x1 := a + b - x2; y1 := func(x1);
if (x2 > x1) and (y2 > y1)
then
begin
b := x2; x2 := x1; y2 := y1; goto 1
end;
if (x2 <= x1) and (y2 > y1)
then
begin
a := x2; x2 := x1; y2 := y1; goto 1
end;
if (x2 > x1) and (y2 < y1)
then
begin
a := x1; goto 1
end;
if (x2 <= x1) and (y2 <= y1)
then
begin
b := x1; goto 1
end;
1: end;
x := (a + b)/2;
write('Мин.
значение функции на (');
writeln(aa:1:0, ',', bb:2:0, ')');
writeln('Значение функции равно ', func(x):6:12);
writeln('При значении аргумента ', x:6:12)
end.
В этой программе число приближений устанавливается пользователем. Программу можно изменить, указав в условии цикла точность приближения значений аргумента x. Но тогда придется каждый раз при повторении цикла изменять коэффициент деления, так неизвестно конечное число повторений цикла. Для этого можно добавить в программу процедуру вычисления границ промежутка:
{ Процедура вычисления знач. аргумента и функции }
{ approach - приближение }
Procedure approach(a, b : real; n : integer; var x2, y2 : real);
begin
x2 := a + (b - a)*fib(n - 1)/fib(n);
y2 := func(x2)
end;
И тогда, программа станет следующей:
{Поиск минимума функции методом Фибоначчи}
Program Minimumfib;
uses WinCrt;
label 1;
var
a, aa, bb, x, b, x1, x2, y1, y2, e : real;
n : integer;
{----------------------------------------------------------------------------------------}
{ Заданная исследуемая функция }
Function func(x : real) : real;
begin
func := x*x*x*x - 14*x*x*x + 60*x*x - 70*x
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления членов ряда Фибоначчи }
Function fib(n : integer) : real;
var
f, f1, f2 : real;
i : integer;
begin
f1 := 1; f := 0;
for i := 1 to n do
begin
f2 := f1;
f1 := f;
f := f1+f2
end;
fib := f
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления знач.
аргумента и функции }
{ approach - приближение }
Procedure approach(a, b : real; n : integer;
var x2, y2 : real);
begin
x2 := a + (b - a)*fib(n-1)/fib(n);
y2 := func(x2)
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write(' Введите нижнюю границу промежутка '); readln(a);
aa := a;
write('Введите правую границу промежутка '); readln(b);
bb := b;
write('Введите точность приближения '); readln(e); n := 3;
approach(a, b, n, x2, y2);
while abs(b - a) > e do
begin
x1 := a + b - x2; y1 := func(x1);
if (x2 > x1) and (y2 > y1)
then
begin
n := n + 1;
approach(a, b, n, x2, y2);
b := x2; x2 := x1; y2 := y1; goto 1
end;
if (x2 <= x1) and (y2 > y1)
then
begin
n := n + 1;
approach(a, b, n, x2, y2);
a := x2; x2 := x1; y2 := y1; goto 1
end;
if (x2 > x1) and (y2 < y1)
then
begin
n := n + 1;
approach(a, b, n, x2, y2);
a := x1; goto 1
end;
if (x2 <= x1) and (y2 <= y1)
then
begin
n := n + 1;
approach(a, b, n, x2, y2);
b := x1; goto 1
end;
n := n + 1;
approach(a, b, n, x2, y2);
1: end;
x := (a + b)/2;
write('Мин. значение функции на промежутке (');
writeln(aa:1:0,',',bb:2:0,')');
writeln('Значение функции равно ', func(x):6:12);
writeln('При значении аргумента ', x:6:12)
end.
Очень часто, при поиске минимума функции для деления отрезка используют так называемое "Золотое сечение".
"Золотое сечение" или "золотое сечение" - деление отрезка на две части так, что большая из них есть средняя пропорциональная между меньшей частью и всем отрезком. Если a - весь отрезок, x - большая из двух частей, тогда:
a : x = x : (a - x)
Решая это уравнение, получаем:


Зная это, можно составить программу поиска минимума функции, используя "золотое сечение", тогда:
x1 := 0.618*a + 0.382*b, x2 := 0.382*a + 0.618*b.
Для вычисления этих значений можно составить две процедуры, которые затем использовать в программе.
Procedure gold1(a, b : real; var
x1, y1 : real);
begin
x1 := 0.618*a + 0.382*b; y1 := fx(x1)
end;
{------------------------------------------------------}
Procedure gold2(a, b : real; var
x2, y2 : real);
begin
x2 := 0.382*a + 0.618*b; y2 := fx(x2)
end;
