Решение уравнений с одной переменной методом половинного деления
Здесь мы очень кратко рассмотрим один из простых методов решения нелинейных уравнений - метод половинного деления, так как другие методы будут рассмотрены позже, после изучения последовательностей, массивов и множеств.
Главная цель этого небольшого раздела - показать использование функций, создаваемых пользователем в программах.
Отделение корней
Первый этап численного решения уравнения f(x) = 0 состоит в отделении корней, т.е. в установлении "тесных" промежутков, содержащих только один корень.
При отделении корней на некотором промежутке [a, b], мы потребуем, чтобы функция f(x) была непрерывна на этом промежутке и будем считать, что все интересующие нас корни находятся на промежутке [a, b], в котором f(a)*f(b) < 0.
Будем вычислять значения функции f(x), начиная с точки x = a, двигаясь вправо с некоторым шагом h. Как только обнаружится пара соседних значений f(x), имеющих разные знаки, и функция f(x) монотонна на этом отрезке, тогда значения аргумента x (предыдущее и последующее) можно считать концами отрезка, содержащего корень. Результатом решения этой задачи будет вывод значений концов промежутка.
Очевидно, что надежность рассмотренного подхода к отделению корней зависит как от характера функции f(x), так и от выбранной величины шага h. Действительно, если при достаточно малом значении h на концах текущего отрезка




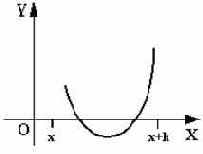
Рис. 24
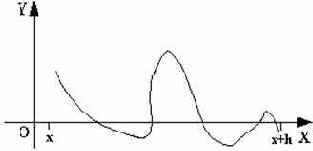
Рис. 25
Предвидя подобные ситуации, следует выбирать при отделении корней достаточно малые значения h.
Давайте посмотрим как будет выглядеть программа отделения корней для функции

Ясно, что необходимо завести функцию, которая бы при необходимости обращения к ней вычисляла ее значения.
Эту функцию мы устроим уже известным нам способом и назовем fx:
Function fx(x : real) : real;
begin
fx := cos(x) - 0.1*x
end;
В основной программе, естественно потребовать от пользователя ввода границ промежутка и шага. В качестве границ промежутка будут переменные a и b, а для шага - h (в качестве значения шага, при выполнении программы возьмем 0.1).
Для подсчета числа промежутков будет служить счетчик k. Первоначальное значение левой границы: x1:=a; а первая правая граница будет равна сумме левой границы и шага: x2:=x1+h; значение функции в левой границе первого промежутка: y1:=fx(x1).
Последовательно к левой границе добавляется шаг h и так должно продолжаться пока
это значение не станет равно правой границе данного промежутка b. Значит, необходимо организовать цикл "пока": while x2 <= b do
В цикле, вычислять значение функции в точке x2, которая уже получилась от увеличения x1 на h: y2 := fx(x2).
Теперь следует проверить знак произведения значений функций на концах промежутка (fx(x1)*fx(x2)) и, если оно отрицательно, то на этом промежутке будет существовать корень, а значит надо выдать на экран координаты этого промежутка и его номер:
if y1*y2 < 0 then
begin
k := k + 1;
writeln(k,'-й корень на [',x1:6:4,'; ',x2:6:4,']')
end;
Далее следует продолжить движение к правой границе, а для этого выполнить следующие операторы:
x1 := x2; x2 := x1 + h; y1 := y2
Вот и вся несложная тактика этой программы. Полностью она приводится ниже:
Program
Separation_root; { Программа отделения корней }
uses WinCrt;
var
a, b, h, x1, x2, y1, y2 : real;
k : integer;
{----------------------------------------------------------------------------------------}
Function fx(x : real) : real;
begin
fx := cos(x) - 0.1*x
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите левую границу промежутка '); readln(a);
write('Введите правую границу промежутка '); readln(b);
write('Введите шаг '); readln(h);
k := 0;
x1 := a; x2 := x1 + h;
y1 := fx(x1);
while x2 <= b do
begin
y2 := fx(x2);
if y1*y2 < 0
then
begin
k := k+1;
writeln(k, '-й корень на [', x1:6:4, ';', x2:6:4, ']')
end;
x1 := x2; x2 := x1 + h;
y1 := y2
end
end.
Следующим, естественным этапом решения, является нахождение на промежутке корень с заданной степенью точности (если, конечно, уже известно, что он существует на нем).
Для этого нетрудно сочинить простую программу вычисления корня методом половинного деления, сущность которого заключается в следующем.
Известно, что на промежутке [a; b] есть корень. Зададим необходимую точность, с которой нам необходимо его вычислить. Обозначим ее - e.
Разделим промежуток [a; b] пополам. Точкой деления будет точка (см. рис. 25)

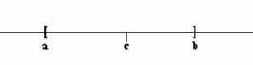
Рис. 25
Установим, на котором из полученных двух промежутков находится корень. Для чего найдем знак разности fx(a)*fx(c). Если этот знак отрицательный, тогда корень находится на левом промежутке. Заменив c на b (b:=c), мы получим новый промежуток, обозначенный прежними буквами (см. рис. 26):
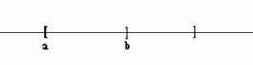
Рис. 26
А если разность fx(a)*fx(c) не будет отрицательной, тогда корень находится на правом промежутке. Заменив c на a (a := c), мы получим новый промежуток для поиска корня, обозначенный теми же буквами (см. рис. 27):
Рис. 27
И такой процесс деления надо выполнять, пока разность между правой и левой границами по абсолютной величине будет больше заданной точности e
(

Пользуясь этими соображениями, нетрудно составить программу, где сам процесс половинного деления будет выполняться с помощью процедуры.
В качестве функции берется функция: f(x) := sin(2*x) - ln(x) и рассматривается на промежутке

После завершения основного цикла, находится окончательное значение x,


Program Division;
uses WinCrt;
var
a, b, c, e, x, d : real;
{----------------------------------------------------------------------------------------}
Function func(x : real) : real;
begin
func := sin(2*x) - ln(x)
end;
{----------------------------------------------------------------------------------------}
Procedure half(a, b, e : real; var x, d : real);
var
c : real;
begin
while abs(b - a) > e do
begin
c := (a + b)/2;
if func(a)*func(c) < 0 then b := c else a := c
end;
x := (a + b)/2;
d := abs(b - a)/2
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите левую границу промежутка '); readln(a);
write('Введите правую границу промежутка '); readln(b);
write('Введите точность вычисления корня '); readln(e);
half(a, b, e, x, d);
writeln('Значение корня равно x = ', x:6:10);
writeln('С границей погрешности ', d:2:10)
end.
Можно объединить программы отделения корня и уточнения его методом половинного деления в одну и получить программу, которая отделяет промежутки и сразу вычисляет на каждом из них корни с заданной точностью.
Программа
Program Equation;
uses WinCrt;
var
a, b, h, x1, x2, y1, y2, e, x, d : real;
k : integer;
{----------------------------------------------------------------------------------------}
Function fx(x : real) : real;
begin
fx := cos(x) - 0.1*x
end;
{----------------------------------------------------------------------------------------}
Procedure half(a, b, e : real; var x, d : real);
var
c : real;
begin
while abs(b - a) > e do
begin
c := (a + b)/2;
if fx(a)*fx(c) < 0 then b := c else
a := c
end;
x := (a + b)/2;
d := abs(b - a)/2
end;
{----------------------------------------------------------------------------------------}
begin
write(' Введите левую границу промежутка '); readln(a);
write('Введите правую границу промежутка '); readln(b);
write('Введите шаг '); readln(h);
write('Введите точность вычисления корня '); readln(e);
k := 0; x1 := a; x2 := x1 + h;
y1 := fx(x1);
while x2 <= b do
begin
y2 := fx(x2);
if y1*y2 < 0
then
begin
k := k + 1;
half(x1, x2, e, x, d);
write(k,'-й корень равен ', x:6:6);
writeln(' с погрешностью ', d:2:10)
end;
x1 := x2; x2 := x1 + h; y1 := y2
end
end.
