Вычисление корней уравнения нахождением минимума функции на промежутке
Зная определение минимума функции на промежутке, легко применить этот метод к нахождению корней уравнения.
Для этого достаточно рассматривать на заданном промежутке не саму функцию, а ее модуль, тогда минимум функции будет находиться на оси OX , а значение аргумента в этой точке даст нам значение корня уравнения на заданном промежутке. Разумеется, функция должна удовлетворять всем вышеперечисленным требованиям.
Ниже приводятся рисунки, которые наглядно показывают механизм применения поиска минимума функции на промежутке к нахождению корней. На одном из рисунков схематически показан график заданной функции, а на втором - график абсолютного значения этой функции применительно к нахождению корня с использованием поиска минимума для нахождения корня (см. рис. 28 и 29).
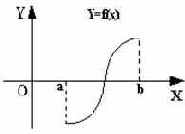
Рис. 28
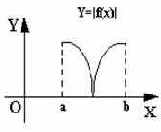
Рис. 29
Программа нахождения корня уравнения с использованием поиска минимума функции методом “золотого сечения” приводится ниже.
{Решение уравнений с использованием определения минимума }
{ с помощью "золотого сечения" }
Program Equation_min_gold;
uses WinCrt;
var
a, a1, b, b1, e, x : real;
{----------------------------------------------------------------------------------------}
{ Поиск минимума функции методом золотого сечения }
Procedure mingold(a, b, e : real; var
x : real);
var
x1, x2, y1, y2 : real;
{----------------------------------------------------------------------------------------}
Function func(x : real) : real;
begin
func := abs(sin(2*x) - ln(x))
end;
{----------------------------------------------------------------------------------------}
Function f1(a, b : real) : real;
begin
f1 := 0.618*a + 0.382*b
end;
{----------------------------------------------------------------------------------------}
Function f2(a, b : real) : real;
begin
f2 := 0.382*a + 0.618*b
end;
{----------------------------------------------------------------------------------------}
begin
x1 := f1(a, b); y1 := func(x1);
x2 := f2(a, b); y2 := func(x2);
while abs(b - a) > e do
if y1<y2 then
begin
b := x2; x2 := x1; y2 := y1;
x1 := f1(a, b); y1 := func(x1)
end
else
begin
a := x1; x1 := x2; y1 := y2;
x2 := f2(a, b); y2 := func(x2)
end;
x := (a + b)/2
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите нижнюю границу промежутка '); readln(a);
a1 := a;
write('Введите правую границу промежутка '); readln(b);
b1 := b;
write('Введите точность вычисления корня ');readln(e);
mingold(a, b, e, x);
write('Корень уравнения на промежутке (');
write(a1:1:0, '; ', b1:2:0, ')');
writeln(' равен x = ', x:6:6);
writeln('с точностью до ',e:2:6)
end.
Задание 5
Составьте программу нахождения корня уравнения, применяя поиск минимума функции с помощью ряда Фибоначчи.
